Fast Radial Basis Function Interpolation
RBF Interpolation is a highly ill-conditioned problem. We develop a stable and fast multiresolution method for solving Radial Basis Function interpolation of datasets in 3 dimensions. To our knowledge, this is the current state of the art solver for linear and higher-order RBF interpolation.
Overview
Details
RBF Interpolation is a highly ill-conditioned problem. We develop a stable and fast multiresolution method for solving Radial Basis Function interpolation of datasets in 3 dimensions. To our knowledge, this is the current state of the art solver for linear and higher-order RBF interpolation. Applications include medical imaging, geophysics, and Kriging (regression). This work is currently being extended to higher dimensions.
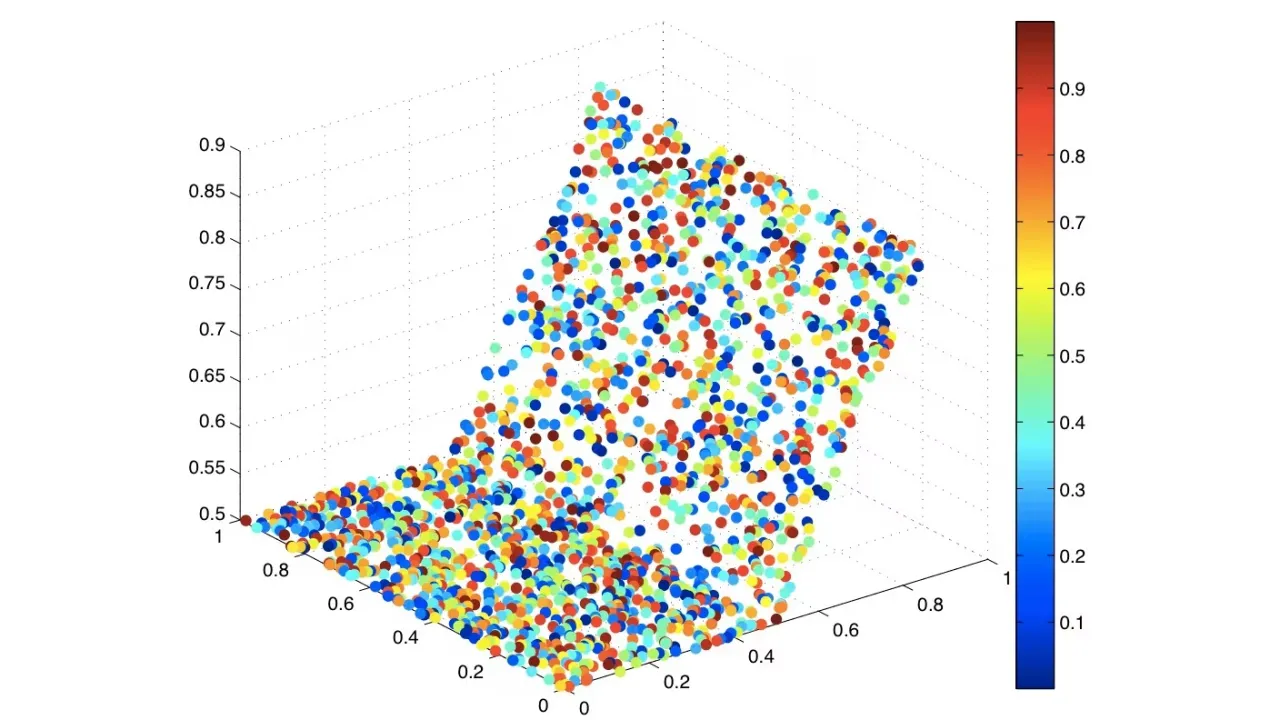
Test Case #1: 4th order polynomial interpolation with biharmonic spline.
The color reflects the function value on the node
Performance Wall Clock Times: Test Case #1: O(N * sqrt(N))
Collaborators
- Julio E. Castrillon Candas
- Jun Li, Schlumberger, 5599 San Felipe, Ste 100, Houston, TX 77056, USA. e-mail: JLi49@slb.com
- V. Eijkhout. Texas Advanced Computing Center, the University of Texas at Austin, Austin, USA. e-mail: eijkhout@tacc.utexas.edu
Publications
- Julio E. Castrillon-Candas, Jun Li, Victor Eijkhout, A discrete adapted hierarchical basis solver for radial basis function interpolation, BIT Numerical Mathematics, Springer, July 2012.
